What Does Regression Analysis Tell You? A Super Simple Explanation

Regression analysis is one of the most important and widely used statistical techniques out there. But for many people, it remains kind of confusing and mysterious.

Well, we’re here to lift the veil on regression analysis and explain exactly what it does in simple terms! Read on for my beginner’s guide to understanding regression analysis.

What is Regression Analysis?

Regression analysis is a statistical method used to estimate the relationship between a dependent variable and one or more independent variables.

In other words, it helps us understand how the value of the dependent variable changes when we change the value of the independent variables. The aim is to determine the “causal effect” of the independent variables on the dependent variable.

Some key terms

• Dependent variable The variable we are trying to explain or predict Also called the “outcome variable”

• Independent variables The variables we think have an effect on the dependent variable Also called “predictor variables” or “explanatory variables”

• Regression coefficient: The metrics that quantify the effect each independent variable has on the dependent variable.

The regression coefficients tell us the size and direction (positive or negative) of the effect.

Why Use Regression Analysis?

There are a few key reasons regression analysis is so popular:

• Determine the strength of relationships between variables. The regression coefficients show us how strongly each independent variable influences the dependent variable.

• Make predictions. We can use the regression equation to predict values of the dependent variable given values of the independent variables.

• Identify the most important independent variables. The size of the regression coefficients tells us which independent variables have the biggest effect.

• Assess impacts of changes. By changing the values for the independent variables in our equation, we can estimate the impact on the dependent variable.

Types of Regression Analysis

The two most common types of regression analysis are:

• Simple linear regression: Estimates the relationship between a single independent variable and the dependent variable.

• Multiple linear regression: Estimates the relationship between multiple independent variables and the dependent variable.

More advanced regression techniques include logistic regression and nonlinear regression. But linear regression models are by far the most common, especially for beginners.

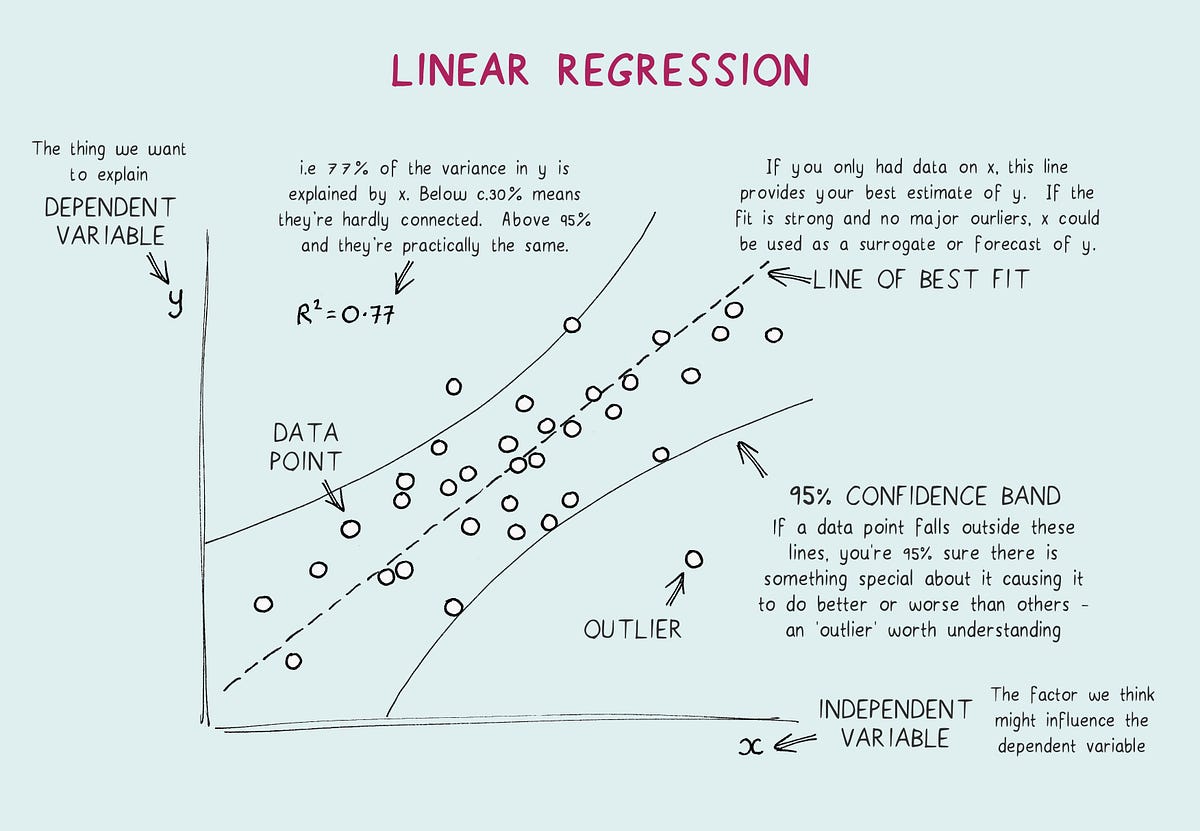
How Does Linear Regression Analysis Work?

Linear regression uses a straight line equation to estimate the relationship between the independent and dependent variables.

The linear regression equation takes the form:

y = a + b1*x1 + b2*x2 + ... + bn*xn

Where:

• y = Dependent variable
• a = Intercept
• b1 to bn = Regression coefficients
• x1 to xn = Independent variables

To perform a linear regression, statistics software calculates the values for the intercept (a) and regression coefficients (b1, b2, etc.) that produce the “best fit” line through the data points.

The most common method is ordinary least squares, which minimizes the sum of the squared residuals (aka the differences between the actual data values and the values predicted by the line).

Once we’ve fit the regression line, we can use the equation to make predictions! We just plug in the values for the independent variables and calculate the estimate for the dependent variable.

Interpreting Regression Coefficients

The key results from a regression analysis are the regression coefficients for each independent variable. These tell us:

• Direction of the effect: A positive coefficient means the dependent variable increases when that independent variable increases. A negative coefficient means the dependent variable decreases when that independent variable increases.

• Size of the effect: The actual value of the coefficients indicates the size of the effect each independent variable has on the dependent variable. Larger coefficients mean the independent variable has a larger impact.

• Statistical significance: Does the independent variable have a real, statistically significant impact on the dependent variable? Or is the effect just random chance? P-values help assess the significance. Lower p-values indicate higher significance.

Real-World Regression Analysis Examples

Here are some examples of how regression analysis is used by businesses, researchers, and policy analysts:

• Estimate how sales are impacted by advertising spend, price changes, promotions, etc.

• Forecast stock returns based on financial ratios like P/E, debt ratios, dividend yield, etc.

• Analyze how different factors contribute to employee turnover.

• Estimate the effect of class size on student test scores.

• Predict the impact of fiscal policy changes on economic growth.

As you can see, regression analysis is applied in tons of different contexts to estimate the causal effect of some factors on key outcomes of interest. It provides critical insights for decision making.

Limitations of Regression Analysis

While an invaluable statistical tool, regression analysis does have some important limitations to be aware of:

• Correlation doesn’t equal causation. Regression analysis estimates relationships between variables, but does not definitively prove causation. There may be other confounding factors affecting your dependent variable.

• Outliers can skew results. Highly influential outliers can distort the best fit regression line. Always plot your data visually to check for outliers.

• Assumptions may be violated. Linear regression analysis relies on certain assumptions that must be validated, such as linearity, normality, homoscedasticity, and lack of multicollinearity. Violating these assumptions can invalidate results.

So regression analysis must always be applied thoughtfully, with careful consideration of the methodology and business context. The estimates provide helpful guidance, but human judgement is still critical.

Let’s Break It Down…

Hopefully this breakdown clarified what regression analysis is all about! To recap:

• Regression analysis estimates the relationships between a dependent variable and one or more independent variables.

• The most common types are simple linear and multiple linear regression.

• It provides the direction and size of effects, helps make predictions, and identifies the most influential factors.

• Regression coefficients and p-values are key outputs to interpret.

• Limitations include lack of definitive causation proof, outliers, and assumptions that may be violated.

Used correctly, regression analysis is an invaluable tool for quantitative analysis and data-driven decision making. And now you know the basics to understand the regression results you encounter day to day!