Scientific notation is a way of expressing numbers that are very large or very small in a concise format. It has many uses in science, engineering, economics and other fields that involve dealing with extreme values. Learning how to write numbers in scientific notation only takes a few simple steps. With practice, you’ll be able to easily convert back and forth between standard decimal notation and scientific notation.
What is Scientific Notation?
In scientific notation, a number is written as the product of a decimal number between 1 and 10 multiplied by a power of 10.
For example:
- 5,000,000 = 5 x 106
- 0.00000065 = 6.5 x 10-7
The decimal number is called the coefficient. The power of 10 is called the exponent.
Scientific notation makes it easy to see the significant digits of a number and determine its order of magnitude at a glance It’s extremely useful for calculations and expressing values concisely
When to Use Scientific Notation
Scientific notation is used when numbers are either
- Very large (over 1000)
- Very small (less than 1)
Some examples of when scientific notation is handy
- Describing astronomical distances (e.g. the Earth is 149.6 x 106 km from the Sun)
- Working with atomic-scale measurements in physics and chemistry
- Writing the values of constants like the speed of light (299,792,458 m/s = 2.99792458 x 108 m/s)
- Dealing with populations, finances, or other vast numbers
Scientific notation lets us express these numbers neatly and precisely. The exponent immediately conveys the scale we’re working with.
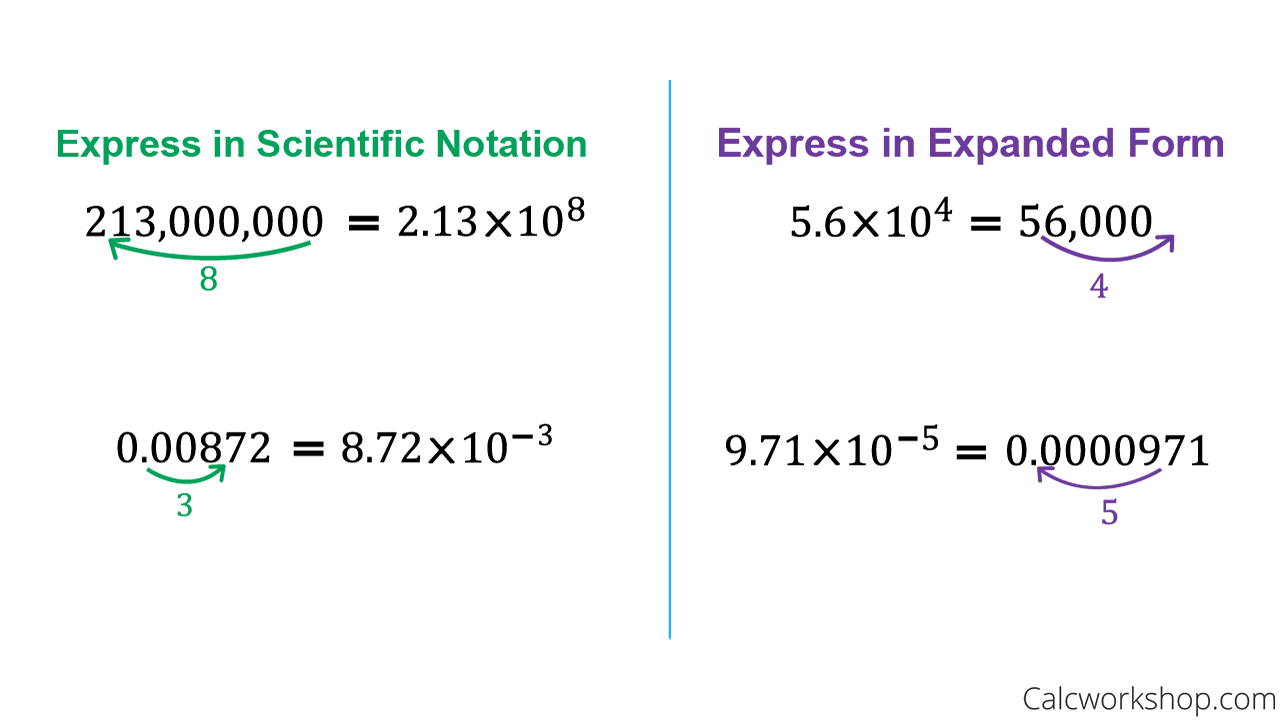
How to Write Large Numbers in Scientific Notation
To express a large number in scientific notation:
-
Identify the first significant digit. For whole numbers, this is simply the first non-zero digit.
-
Move the decimal point after that first significant digit to create a number between 1 and 10.
-
Count the number of digits after the decimal point. This is the exponent that 10 will be raised to.
For example, to write 589,000 in scientific notation:
-
The first significant digit is 5.
-
We move the decimal to make 5.89.
-
There are 5 digits after the decimal point.
So, 589,000 = 5.89 x 105
The exponent of 105 tells us there are 5 digits after the first significant digit. Scientific notation clearly shows the order of magnitude of this number.
How to Write Small Numbers in Scientific Notation
To express a small decimal in scientific notation:
-
Ignore any leading zeros and identify the first significant digit.
-
Move the decimal point after that digit to make a number between 1 and 10.
-
Count the number of digits before that significant digit. Make the exponent negative and equal to that number.
For example, to write 0.00000314 in scientific notation:
-
The first significant digit is 3.
-
We move the decimal to make 3.14.
-
There are 5 leading zeros before the 3.
So, 0.00000314 = 3.14 x 10-5
The negative exponent -5 indicates the number of leading zeros. This quickly shows the order of magnitude of the small number.
Examples
Let’s look at some examples to get familiar with writing large and small numbers in scientific notation:
Large Number| Scientific Notation
Where is scientific notation used?
Scientific notation is often used in the fields of science and math. Instead of writing a number in standard form with many zeros, mathematicians and scientists often prefer to condense numbers into scientific notation because it is much more compact. For example, the number (4{,}000{,}000{,}000{,}000) can be written as (4times10^{12}). This form makes extremely large and extremely small numbers easier to work with.
When should you use scientific notation?
Scientific notation should be used when doing calculations with numbers that are extremely large or extremely small. Chemists often use scientific notation when dealing with extremely small measurements. Astronomers often use scientific notation when dealing with extremely large measurements.
Scientific Notation – Fast Review!
How do you write a number in scientific notation?
Numbers written in scientific notation must adhere to the following rules: The number before the multiplication sign must always be at least 1 and less than 10. There is always a multiplication by a power of 10 (as opposed to a multiplication by any other number). The power of 10 can be negative, zero or positive.
What is scientific notation used for?
Scientific notation is generally used with very large or very small numbers in applications such as physics, engineering, and chemistry. It condenses the numbers into a number a between 1 (included) and 10 (excluded) multiplied by 10 raised to an exponent, denoted as a × 10ⁿ.
How to compare a number written in standard notation to scientific notation?
When comparing a number written in standard notation to a number written in scientific notation, it may also be referred to as ‘expanded form’. The first step is to write the first part of the number which must always be between 1 and 10. We take 32500 and write it as 3.25 so that it is now a number that is bigger than 1 and less than 10.
What is a number not written in scientific notation?
The name for a number not written in scientific notation is simply ‘standard notation’ or ‘decimal notation’. When comparing a number written in standard notation to a number written in scientific notation, it may also be referred to as ‘expanded form’. The first step is to write the first part of the number which must always be between 1 and 10.