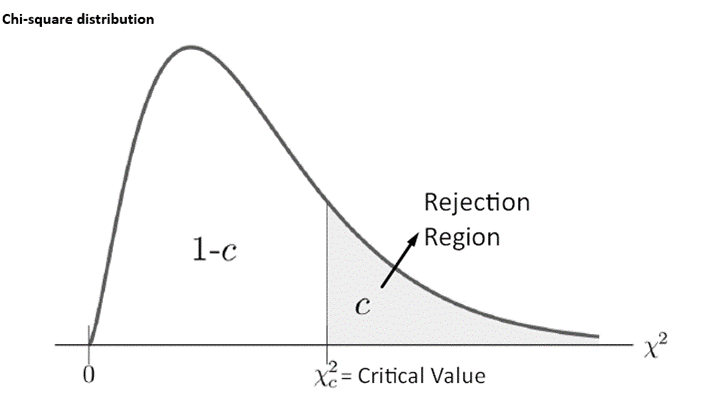
The chi-square critical value is a statistical value used in the chi-square test to determine whether the differences between observed and expected data are significant. In simpler terms, it is like a threshold that helps in determining if the relationship between categorical variables in a study is real or if it could likely occur randomly.
The critical value of Chi-square is determined based on the degree of freedom and significance level. In statistical notation, chi-square is denoted by χ2. It is important to note that the symbol χ differs from the standard letter X.
In this article, we are going to explore the concept of chi-square critical value that is often tested in IB Maths AI at both SL and HL. We will learn how to find out the critical value of the chi-square and how to use it in the chi-square test. Moreover, we will solve some examples of finding chi-square to help in better understanding.
Critical values are an important concept in statistical analysis, allowing you to determine the significance of your results. But for many students and researchers, calculating and interpreting critical values can be confusing.
In this comprehensive guide, I’ll walk you through the key steps for finding critical values and using them to draw conclusions from your data Whether you’re comparing means or calculating correlations, this article will equip you with a clear understanding of critical values
What is a Critical Value?
In statistics the critical value is the boundary for determining whether to reject or fail to reject the null hypothesis based on your calculated test statistic. Let’s break that definition down
-
The null hypothesis is the default statement that there is no relationship between two measured phenomena. It is denoted H0.
-
The test statistic is a value calculated from sample data during a hypothesis test such as a t-statistic in a t-test.
-
The critical value acts as a cutoff point on the test statistic distribution. If the calculated test statistic falls beyond the critical value, the null hypothesis can be rejected.
For example, if your test statistic is larger than the critical value, you can reject the null hypothesis and conclude there is a statistically significant effect or relationship within the data.
Critical values are dependent on your selected significance level (also called alpha level). Common significance levels are 5% (0.05), 1% (0.01) and 0.1% (0.001). The lower the significance level, the harder it is to reject the null hypothesis.
How to Find Critical Values
Here are the key steps for determining the critical value for your statistical test:
-
Find the alpha level
- Select your significance level, usually 0.05, 0.01 or 0.001. This is your alpha value.
-
Determine degrees of freedom
- The degrees of freedom depends on sample size for t-tests and ANOVA, or number of variables for chi-square tests.
-
Look up critical value
- Using a t-table, F-table or other statistical table, locate the critical value that corresponds to your alpha and degrees of freedom.
-
Use two-tailed vs one-tailed
- For two-tailed tests, match the alpha value. For one-tailed, find the value corresponding to alpha/2.
These tables allow you to look up the critical values for different statistical tests based on alpha and degrees of freedom. With the critical value determined, you can now evaluate the significance of your test statistic.
Comparing Test Statistic to Critical Value
Once you’ve calculated a test statistic, like a t-value, F-value or chi-square value, compare it to the critical value:
-
If the test statistic is in the critical region beyond the critical value, reject the null hypothesis. Your results are statistically significant.
-
If the test statistic falls within the acceptance region inside the critical value, fail to reject the null hypothesis. Your results are not statistically significant.
For example, with an alpha of 0.05 and 20 degrees of freedom, the t-critical value is 2.086. If your calculated t-statistic is -3.12, it falls in the critical region. Therefore, you can reject the null hypothesis and conclude the test reveals a statistically significant difference between groups.
Worked Examples
Let’s walk through a few examples of finding and applying critical values:
t-test Example
- H0: There is no difference in test scores between males and females
- α = 0.05
- t-statistic = 2.46
- Sample 1 n = 25
- Sample 2 n = 25
- Degrees of freedom = 48 (n1 + n2 – 2)
Using a t-table:
- α = 0.05
- DF = 48
- Critical value = 2.0106
Since the t-statistic of 2.46 exceeds the critical value of 2.0106, we reject the null hypothesis. There is a statistically significant difference between male and female test scores.
ANOVA Example
- H0: There is no difference in crop yield between organic and chemical fertilizers
- α = 0.01
- F-statistic = 9.28
- Groups: A, B, C, D
- Degrees of freedom: Between groups = 3; Within groups = 16
Using an F-table:
- α = 0.01
- DFbet = 3
- DFwith = 16
- Critical value = 4.49
Since the F-statistic of 9.28 exceeds the critical value of 4.49, we reject the null hypothesis. There are statistically significant differences in crop yield across the fertilizer groups.
Chi-Square Example
- H0: Candidate preference is independent of voter age
- α = 0.05
- Chi-square statistic = 12.04
- Degrees of freedom = 6
Using a chi-square table:
- α = 0.05
- DF = 6
- Critical value = 12.59
Since the chi-square statistic of 12.04 does not exceed the critical value of 12.59, we fail to reject the null hypothesis. There is no statistically significant association between voter age and candidate preference.
When to Use One-Tailed vs Two-Tailed Critical Values
Some final advice:
-
Use a one-tailed critical value when testing for differences in a single direction (e.g. crop yield is higher with fertilizer).
-
Use a two-tailed critical value when testing for differences in either direction (e.g. test scores could be higher for either gender).
Keep this in mind when looking up critical values in statistical tables for different tests. Understanding if your hypothesis is directional or not will ensure you find the right critical value threshold.
By mastering how to accurately calculate and apply critical values, you can determine whether your experiment or study results are statistically significant. A simple mathematical concept with an important role in scientific analysis!
FAQs about Critical Values
What happens if the test statistic equals the critical value exactly?
In this case, the result would still be considered statistically significant, since the critical value marks the cutoff threshold.
Should I use a z-table or t-table to find critical values?
Use a z-table when the population standard deviation is known. Use a t-table when the population standard deviation is unknown and you have to rely on a sample standard deviation.
Why are degrees of freedom important for critical values?
Critical values are different for varying degrees of freedom. More degrees of freedom leads to narrower confidence intervals and smaller critical values.
Can I look up critical values for correlations?
Yes, you would locate the critical value for a Pearson or Spearman correlation coefficient based on your alpha level and sample size, which determines the degrees of freedom.
Hopefully this article has reduced some of the uncertainty around calculating and applying critical values in statistical hypothesis testing. Be sure to practice finding critical values for different common tests to improve your skills. And don’t hesitate to refer back to examples if you ever need a quick refresher!

How to Calculate Chi-Square Critical Value?
Follow the following three steps to calculate chi square critical value for the desired hypothesis test through the statistical table.
Define the Significance Level (Alpha)
The level of significance (indicated by α) is the probability of rejecting the null hypothesis (H0) when it is true. Commonly used values for alpha are 0.05, 0.01, or 0.10.
Identify the Degrees of Freedom
Degrees of freedom (df) in chi-square tests are determined by the number of categories or groups minus one. It depends on the types of chi-square tests.
df = (rows − 1) × (columns − 1).
Look up the chi-square distribution table
Use a chi-square distribution table to find the critical value of chi-square for the degrees of freedom and level of significance. Find the intersection of the row corresponding to the degrees of freedom and the column corresponding to the chosen significance level (alpha).
The interstation of its row and column is χ2– critical value.
What is Chi-Square Critical Value?
The chi-square test uses the critical value of chi-square to identify whether there is a significant relationship between categorical variables. To do this, the χ² critical value is compared with the statistical test result. This comparison helps decide whether the observed data distribution varies significantly from the expected distribution. Researchers can use it to make statistical inferences about the relationship between categorical variables.
The critical value essentially sets a threshold for the alpha level at which one would reject the null hypothesis. The null hypothesis is rejected if the calculated chi-square test statistic exceeds the χ2 critical value. This implies that the observed data deviates significantly from the expected distribution.
On a graph, the chi-square critical value cut the χ2 distribution into the acceptance and rejection region.