What is Mean Variance Analysis: A Complete Guide

Mean variance analysis is an important concept in investing and portfolio management It helps investors make decisions about which assets to include in their portfolio based on the risk and expected return of each asset. This article provides a complete guide to understanding mean variance analysis

What is Mean Variance Analysis?

Mean variance analysis is a method used to determine the expected risk and return of an investment portfolio. It allows investors to evaluate a portfolio’s asset allocation by assessing the tradeoff between risk and return.

The mean in mean variance analysis refers to the expected return of the portfolio. The variance refers to the variability or volatility of returns around the mean. A portfolio with high variance has more risk because its returns fluctuate more widely.

By analyzing the mean and variance of a portfolio, investors can construct optimal portfolios that provide the highest expected return for a given level of risk. Alternatively, they can create a portfolio with the lowest risk for an expected level of return.

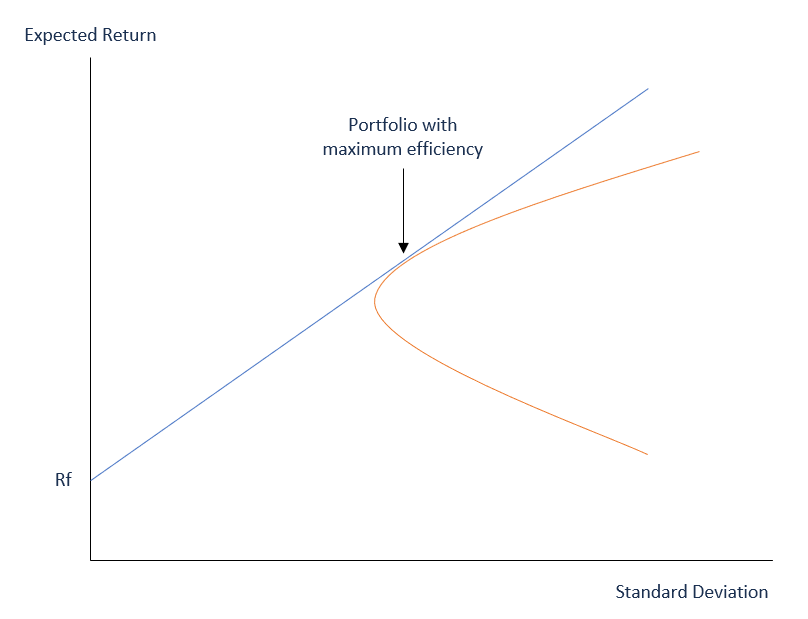
Mean variance analysis is a key component of modern portfolio theory. It suggests that investors are risk averse and aim to maximize returns while minimizing risk. By diversifying investments across asset classes and sectors, investors can build an optimal portfolio.

Main Components of Mean Variance Analysis

There are two primary inputs in mean variance analysis:

Expected Return

This is the anticipated percentage return from an investment. To calculate a portfolio’s expected return, multiply each asset’s weight in the portfolio by its expected return. Then sum the results.

For example, if a portfolio consists of 50% Asset A with a 10% expected return and 50% Asset B with a 5% expected return, the portfolio’s expected return is:

(0.50 x 10%) + (0.50 x 5%) = 7.5%

Variance

Variance measures the spread of returns around the average return. The greater the variance, the more volatile the investment’s performance. Variance is calculated by squaring the standard deviation of returns.

To find the portfolio variance, take each asset’s weight squared and multiply it by the asset’s variance. Then determine the covariance between each pair of assets and multiply it by the weights. Finally, sum the results.

Key Steps in Mean Variance Analysis

Conducting a mean variance analysis involves several key steps:

Determine the expected return for each asset based on historical performance or future return assumptions.
Calculate the variance for each asset using historical return data.
Find the weights allocated to each asset in the portfolio.
Multiply the expected returns by the weights to find the portfolio’s total expected return.
Multiply the variances and covariances by the squared weights to determine the portfolio variance.
Evaluate and optimize the portfolio’s risk-return characteristics. Adjust the asset weights to achieve the desired balance.

Mean Variance Analysis Example

Let’s walk through a simple example of mean variance analysis for a portfolio with two assets:

Stock A has an expected return of 7% and a variance of 0.03. It represents 60% of the total portfolio value.
Stock B has an expected return of 10% and a variance of 0.05. It represents 40% of the total portfolio value.

First, calculate the expected return of the overall portfolio:

Stock A return = 7%
Stock A weight = 60%
Stock B return = 10%
Stock B weight = 40%

Portfolio expected return = (0.60 x 7%) + (0.40 x 10%) = 8.2%

Next, determine the portfolio variance:

Stock A variance = 0.03
Stock A weight squared = (0.60)2 = 0.36
Stock B variance = 0.05
Stock B weight squared = (0.40)2 = 0.16
Covariance(A,B) = 0.006
Weight(A) x Weight(B) = 0.60 x 0.40 = 0.24

Portfolio variance = (0.36 x 0.03) + (0.16 x 0.05) + (2 x 0.24 x 0.006) = 0.012

By analyzing the mean and variance, we can evaluate this portfolio’s risk-return profile. The expected return is 8.2% and the variance is 0.012. By adjusting the asset allocation, we could achieve a different balance of risk and return.

Uses and Limitations of Mean Variance Analysis

Mean variance optimization is widely used in portfolio management. It provides an analytical framework for asset allocation decisions. However, the model makes some simplifying assumptions that investors should consider:

Uses

Optimize portfolio asset allocation and construction
Maximize returns for a given risk level
Minimize risk for a target return level
Quantify and compare portfolios by risk-adjusted return

Limitations

Requires accurate expected return forecasts
Uses variance as the sole risk measure
Assumes returns follow a normal distribution
Doesn’t account for all real-world constraints
Optimized portfolios can be highly concentrated

While a useful tool, mean variance analysis should not be viewed in isolation. Investors should supplement it with additional portfolio modeling, risk analysis, and common sense.

Mean Variance Analysis vs. Other Risk Metrics

Variance is one way to measure investment risk, but not the only method. Here’s how it compares to other common risk metrics:

Standard deviation – The most popular risk metric. It equals the square root of variance.
Beta – Measures asset correlation to the overall market. High beta means more volatility.
Value at risk (VaR) – Estimates potential losses over a period at a confidence level.
Maximum drawdown – Largest historical peak-to-trough decline of an asset.
Sharpe ratio – Calculates risk-adjusted return using standard deviation.

Each risk metric has pros and cons. Variance’s advantage is that it can be mathematically optimized. But standard deviation is more intuitive for many investors.

Implementing Mean Variance Analysis

There are various ways investors can conduct mean variance analysis:

Spreadsheet models – Build a model using Excel or Google Sheets. This allows full control over the methodology.
Portfolio modeling software – Solutions like Bloomberg Portfolio & Risk Analytics include optimized asset allocation tools.
Online calculators – Some robo-advisors and investment sites have free mean variance calculators.
Professional services – Wealth managers often provide mean variance portfolio optimization services.

For large portfolios, advanced software and services provide more robust analysis. But retail investors can easily do basic mean variance modeling with free online tools or spreadsheets.

Key Takeaways on Mean Variance Analysis

Mean variance analysis evaluates a portfolio’s expected return versus risk to optimize the asset allocation.
The mean is the expected return and variance measures return volatility.
By diversifying assets with varied correlations, investors can construct optimal portfolios.
The method has limitations so practical judgement should supplement the quantitative analysis.
Spreadsheets, software, calculators, and advisors can all implement mean variance modeling.

what is mean variance analysis

Mean-Variance Analysis – Example: Calculating Expected Return

Assume a portfolio comprised of the following two stocks:

Stock A: $200,000 with an expected return of 5%. Stock B: $300,000 with an expected return of 7%.

The total value of the portfolio is $500,000, and the weight of each stock is as follows:

Stock A = $200,000 / $500,000 = 40%

Stock B = $300,000 / $500,000 = 60%

The expected rate of return is obtained as follows: = (40% x 5%) + (60% x 7%) = 2% + 4.2% = 6.2%

When creating an investment strategy, the goal of every investor is to create a portfolio of stocks that offer the highest long-term returns without getting into high levels of risk. Modern Portfolio Theory, which includes mean-variance analysis, is based on the idea that investors are risk-averse. Therefore, they focus on creating a portfolio that optimizes the expected return according to a specific level of risk. Investors understand that risk is an inherent part of high-return stocks. The solution for minimizing risk is to diversify the investment portfolio.

A portfolio can be comprised of stocks, bonds, mutual funds, etc., which when combined, come with varying levels of risk. If one security decreases in value, ideally, the loss is compensated by a gain in another security.

A portfolio comprised of various types of securities is considered a better strategic move, as compared to a portfolio comprised of only one type of security. Mean-variance analysis can be an important part of an investment strategy.

Thank you for reading CFI’s guide on Mean-Variance Analysis. To keep learning and advancing your career, the following resources will be helpful:

Share this article

Main Components of Mean-Variance Analysis

Mean-variance analysis is comprised of two main components, as follows:

Variance measures how distant or spread the numbers in a data set are from the mean, or average. A large variance indicates that the numbers are further spread out. A small variance indicates a small spread of numbers from the mean.

The variance may also be zero, which indicates no deviation from the mean. When analyzing an investment portfolio, variance can show how the returns of a security are spread out during a given period.

The second component of mean-variance analysis is expected return. This is the estimated return that a security is expected to produce. Since it is based on historical data, the expected rate of return is not 100% guaranteed.

If two securities offer the same expected rate of return, but one comes with a lower variance, most investors prefer that security.

Similarly, if two securities show the same variance, but one of the securities offers a higher expected return, investors opt for the security with the higher return. When trading multiple securities, an investor can choose securities with different variances and expected returns.

Mean Variance Portfolio Theory Simply Explained

What is mean-variance analysis?

Mean-variance analysis is one part of modern portfolio theory, which assumes that investors will make rational decisions about investments if they have complete information. One assumption is that investors seek low risk and high reward. There are two main components of mean- variance analysis: variance and expected return.

What is variance analysis?

Variance analysis can be summarized as an analysis of the difference between planned and actual numbers. The sum of all variances gives a picture of the overall over-performance or under-performance for a particular reporting period. For each item, companies assess their favorability by comparing actual costs to standard costs in the industry.

What are the components of Mean Variance analysis?

There are two main components of mean- variance analysis: variance and expected return. Variance is a number that represents how varied or spread out the numbers are in a set. For example, variance may tell how spread out the returns of a specific security are on a daily or weekly basis.

How do you calculate mean-variance?

Here is the formula: Variance = number of data points − (the differences between each data point in the data set – the mean)² / (number of data points in the set) Why is mean-variance analysis important? Mean-variance analysis is important because it helps the investor measure an asset’s risk.