Understanding Type I and Type II Errors: A Key Concept in Statistics

As a blogger writing about statistics I often get asked to explain the difference between type I and type II errors. These two types of errors are fundamental concepts in statistical hypothesis testing yet they can be tricky to understand for those without a statistics background. In this article, I’ll explain type I and II errors in simple terms, provide clear examples, and discuss why properly handling these errors is so important in scientific research and data analysis.

What Are Type I and Type II Errors?

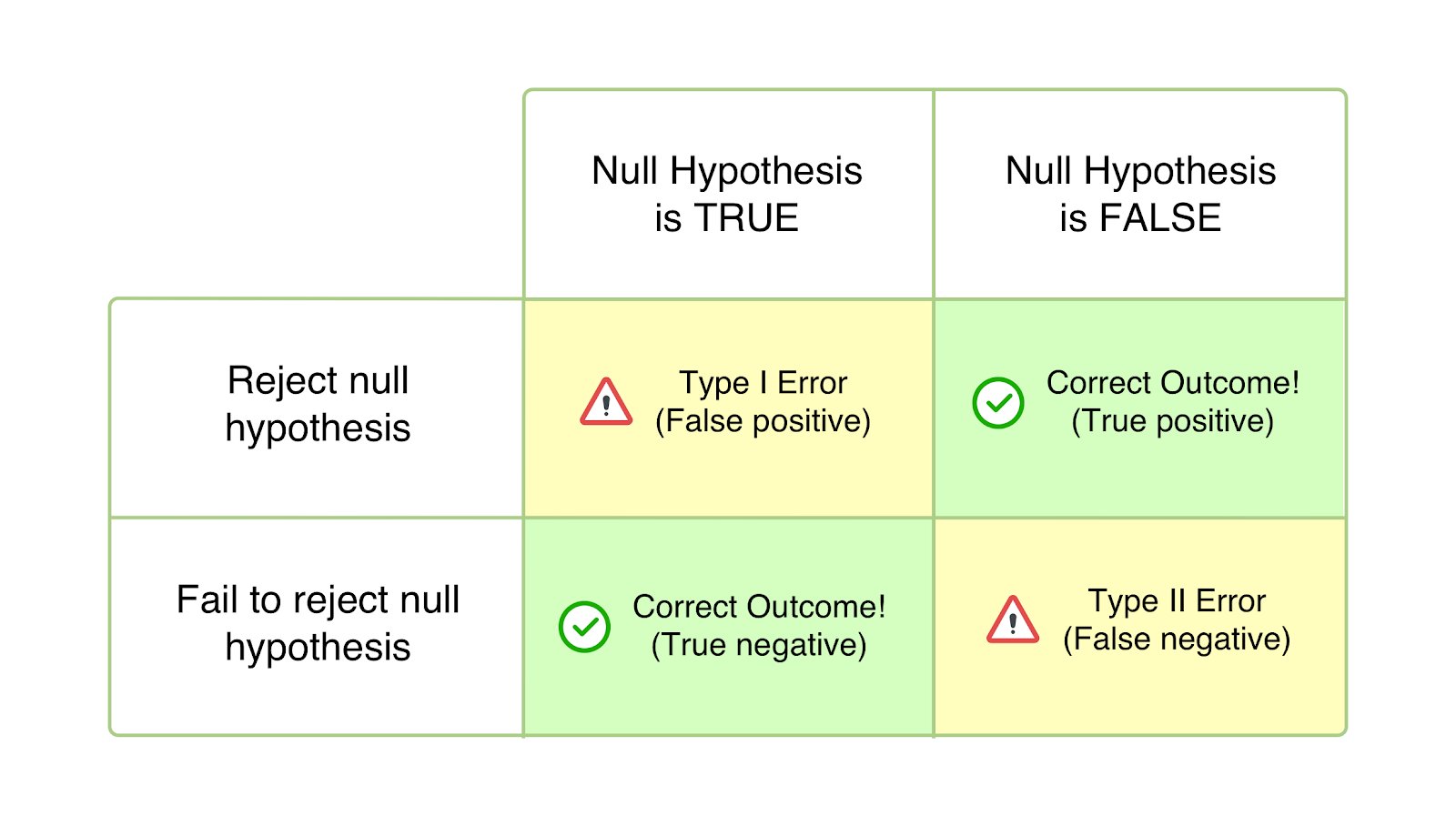
In statistics, we often want to test some claim or “hypothesis” about a population. To do this, we take a random sample from that population and use it to either reject or fail to reject the hypothesis. A type I error means we rejected the hypothesis when we shouldn’t have – it was actually true. A type II error means we failed to reject the hypothesis when we should have – it was actually false.

To understand this, let’s look at a simple example. Say we hypothesize that a new medical treatment is effective. We test this claim by giving the treatment to 50 randomly selected patients and seeing how many improve. If more than 30 patients improve, we will reject the hypothesis and conclude the treatment doesn’t work. If 30 or fewer improve, we will fail to reject the hypothesis and say the treatment is effective.

There are two ways our test could be wrong

• Type I error: The treatment truly is effective, but by chance, fewer than 30 patients improve in our sample. We incorrectly reject the hypothesis.

• Type II error: The treatment is ineffective, but by chance, more than 30 patients improve in our sample. We fail to reject the hypothesis when we should have rejected it.

So in plain language:

• Type I error: False alarm. Concluding something is true when it actually isn’t.

• Type II error: Missing a discovery. Concluding something is false when it is actually true.

Why These Errors Matter

Mistakes happen in statistics – that’s the nature of using samples rather than populations. But we want to design studies that minimize the chances of each error type. Getting the balance right matters:

• Too many type I errors waste time and resources on false leads. We might proclaim dozens of new medical treatments as effective when they actually don’t work.

• Too many type II errors mean we miss out on important discoveries. Truly groundbreaking treatments may be discarded as ineffective due to the study design.

Researchers have to consider the relative harms of each error type for that particular field and topic. In medical testing, a type II error (approving an ineffective treatment) is usually considered worse than a type I error (rejecting an effective treatment). But for law enforcement, a type I error (false conviction) may be viewed as worse than a type II error (letting a criminal go free).

Real World Examples

Let’s look at some real situations where these errors can cause problems:

• Medical screening: Screens like mammograms aim to detect disease early. But they can spur type I errors, false positives that lead to unnecessary tests and procedures. In the US, up to 15% of mammograms produce false positives.

• Drug trials: When testing a new medication, misclassifying an ineffective drug as effective (type II error) can expose patients to useless or harmful treatments. But rejecting an effective drug (type I error) deprives patients of potential cures.

• Justice system: Convicting an innocent person (type I error) is considered a grave miscarriage of justice. But letting a criminal go free (type II error) also has serious consequences for public safety.

Tips for Handling These Errors

So how can researchers design studies to balance type I and II risks appropriately? A few tips:

• Set a higher significance level (often 0.05 or 0.01) to reduce type I errors. This means we’ll only reject the hypothesis with strong evidence.

• Increase the sample size to lower the chance of type II errors. Large samples give us more power to detect effects.

• Use a one-tailed test when an effect in one direction is of interest. This offers more power than a two-tailed test.

• Select the optimal threshold for diagnostics that classify subjects. Lower thresholds reduce type II errors but raise type I errors.

The Takeaway

Type I and II errors are fundamental concepts in statistics, representing false positives and false negatives in hypothesis testing. Carefully balancing these risks is crucial for sound scientific research and informed decision making. Though eliminating these errors entirely isn’t possible, understanding how to minimize them helps us design rigorous studies and interpret results appropriately. With this knowledge, we can push forward human understanding while avoiding foolish conclusions!