The tutorial explains the essence of the standard deviation and standard error of the mean as well as which formula is best to be used for calculating standard deviation in Excel.
In descriptive statistics, the arithmetic mean (also called the average) and standard deviation and are two closely related concepts. But while the former is well understood by most, the latter is comprehended by few. The aim of this tutorial is shed some light on what the standard deviation actually is and how to calculate it in Excel.
Standard deviation is a commonly used statistic that measures how spread out numbers are in a data set. It gives you an idea of how much variation there is from the average value. Excel makes it easy to find standard deviation, thanks to built-in functions. In this comprehensive guide I’ll show you step-by-step how to calculate standard deviation in Excel using the easiest method.
What is Standard Deviation?
In simple terms, standard deviation tells you how much the values in a data set vary from the mean.
A low standard deviation means that the data points tend to be clustered closely around the mean value. A high standard deviation indicates that the data is more spread out from the average.
Here’s an example to understand this better
Let’s say we have two data sets of student test scores:
Data Set 1 65. 68 70 70. 71. 72. 73. 74. 74. 75
Data Set 2:
45, 55, 56, 67, 68, 78, 84, 85, 90, 99
The mean (average) score in Set 1 is 71.
The mean score in Set 2 is also 71.
But the standard deviation of Set 1 is 3.16, while the standard deviation of Set 2 is 16.40.
The low standard deviation in Set 1 tells us that most of the scores are close to the average of 71. But in Set 2, there is a wider variation in the scores.
So although both sets have the same mean, the standard deviation gives us insight into how spread out the data is from the average.
Knowing the standard deviation helps you understand the dispersion, spread and variability in a data set. This is useful in statistics, data analysis, science experiments and more.
How to Calculate Standard Deviation in Excel
There are a few different ways to find standard deviation in Excel. The easiest method is using the built-in STDEV function.
Let’s see how to use the STDEV functions to find standard deviation for a sample data set:
Step 1: Enter the sample data
- Put the data in a single column. For example in cells A1 through A10.
Step 2: Click an empty cell where you want the result
- Let’s say cell B1.
Step 3: Type =STDEV()
- Start by typing =STDEV(
- Next, select the cell range A1:A10
- Close parenthesis to complete the formula =STDEV(A1:A10)
Step 4: Press Enter
This will calculate and display the standard deviation for the sample data set.
The steps are the same if you want to use the STDEV.S or STDEV.P functions instead.
Let’s understand this in more detail…
Excel Formulas for Calculating Standard Deviation
There are a total of 6 standard deviation formulas in Excel:
- STDEV
- STDEV.S
- STDEV.P
- STDEVA
- STDEVPA
- STDEVP
The main ones you’ll use are:
- STDEV.S – Calculates standard deviation based on a sample. Ignores text and logical values.
- STDEV.P – Calculates standard deviation based on the entire population. Ignores text and logical values.
Some key points on when to use each one:
-
Use STDEV.S when calculating the standard deviation of a sample from a larger population. This is the most common scenario.
-
Use STDEV.P if you have data on the entire population and want to find standard deviation.
-
The STDEV function is kept for compatibility with old Excel versions. It is the same as STDEV.S.
-
STDEVA and STDEVPA include text and logical values in the calculation.
-
STDEVP is an old version kept for compatibility. Avoid it.
Now let’s see some examples of using the STDEV and STDEV.S functions to find standard deviation in Excel:
Example 1 – Using STDEV.S on sample data
Let’s calculate the standard deviation for the sample data set below:
| Speed (km/hr) |
|-|-|
| 52 |
| 55 |
| 48 |
| 50 |
| 53 |
| 57 |
| 54 |
The formula is:
=STDEV.S(A2:A8)
This returns a standard deviation of 3.08.
Example 2 – Using STDEV on sample data
Suppose you have the following sample data:
| Sales |
|---|
| 243 |
| 255 |
| 251 |
| 242 |
| 245 |
| 260 |
| 270 |
The formula is:
=STDEV(A2:A8)
This gives a result of 10.10
The STDEV.S and STDEV function give the same result on sample data. Use whichever is available in your version of Excel.
Example 3 – Using STDEV.P on population data
Let’s say you surveyed all 100 students in your class and have their test scores in Excel.
To find the standard deviation for the entire population, use STDEV.P:
=STDEV.P(A2:A101)
This will include all 100 data points in the calculation.
Calculating Standard Deviation of Non-Adjacent Cells
The examples above covered finding standard deviation for a range of adjacent cells.
You can also use the STDEV functions for a few scattered cells that are not next to each other.
For example:
=STDEV(A1, A5, A7)
This will find standard deviation for only cells A1, A5 and A7.
Standard Deviation of Frequency Distribution
Sometimes you may have data with frequency counts, like this:
| Number | Frequency |
|---|---|
| 10 | 5 |
| 15 | 11 |
| 20 | 9 |
| 25 | 12 |
| 30 | 7 |
To find standard deviation:
- Add a column with the frequency multiplied by the numbers
- Use STDEV on this new column
| Number | Frequency | Frequency*Number |
|---|---|---|
| 10 | 5 | 50 |
| 15 | 11 | 165 |
| 20 | 9 | 180 |
| 25 | 12 | 300 |
| 30 | 7 | 210 |
The standard deviation formula is:
=STDEV(C2:C6)
This results in a standard deviation of 7.64.
So this is how you can calculate standard deviation for frequency distributions as well in Excel.
Finding Standard Deviation of Entire Column
You can use the STDEV function on an entire column of data rather than selecting a cell range.
For example:
=STDEV(A:A)
This will find the standard deviation for all cells with data in column A.
An advantage is you don’t have to update the cell range if you add more data to the column. The standard deviation calculation will automatically update.
But there is a disadvantage. The STDEV function will include empty cells in columns selected this way. So it is better to specify the cell range.
Calculating Standard Deviation in Pivot Tables
Pivot tables have a built-in option to calculate standard deviation.
Simply put the field you want in the Values area and change the value field setting to StdDev.
The standard deviation for the underlying data will appear in the pivot table.
And the best part is the value will update automatically even if the source data changes.
Using Standard Deviation for Statistical Analysis
Knowing the standard deviation is useful for statistical analysis and data science applications.
Here are a few examples:
-
Determine normal range: In our test score example earlier, we can deduce that most students scored within 2 standard deviations from the mean. This is the empirical rule that applies for normal distributions.
-
Identify outliers: Data points that are way outside the normal range may be outliers that need special attention.
-
Compare variability: The standard deviation can be used to compare the variability in different data sets, like we did with the two student score examples.
-
Statistical modelling: Standard deviation is used in predictive models to determine confidence levels and prediction intervals.
-
Quality control: Processes where the output should be within a tight range can be monitored using standard deviation. A high standard deviation may indicate issues.
As you can see, standard deviation has many uses in statistical analysis and data science. Excel makes it easy to find standard deviation so you can focus on interpreting the results.
Standard Deviation Chart in Excel
To visualize the spread of data, you can create a standard deviation chart in Excel.
It will show the mean as well as 1, 2 and 3 standard deviations on a bar graph.
Here are the steps to create it:
- Select the data
2
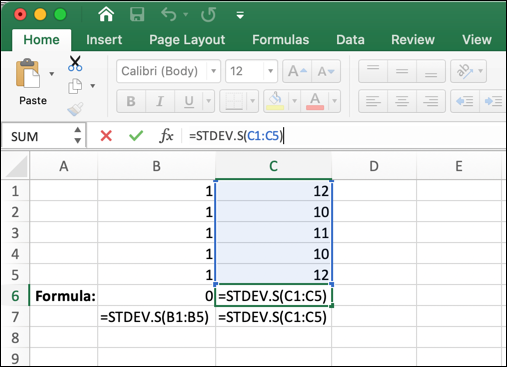
Understanding the standard deviation formula
The reason the nature of the data matters is because the population standard deviation and sample standard deviation are calculated with slightly different formulas:
Sample standard deviation |
Population standard deviation |
Where:
- xi are individual values in the set of data
- x is the mean of all x values
- n is the total number of x values in the data set
Having difficulties with understanding the formulas? Breaking them down into simple steps might help. But first, let us have some sample data to work on: 
First, you find the mean of all values in the data set (x in the formulas above). When calculating by hand, you add up the numbers and then divide the sum by the count of those numbers, like this:
To find mean in Excel, use the AVERAGE function, e.g. =AVERAGE(A2:G2)
This is the part of the standard deviation formula that says: (xi – x)2
To visualize whats actually going on, please have a look at the following s.
In this example, the mean is 5, so we calculate the difference between each data point and 5. 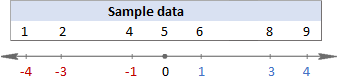
Then, you square the differences, turning them all into positive numbers: 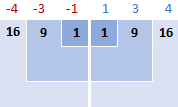
To say “sum things up” in mathematics, you use sigma Σ. So, what we do now is add up the squared differences to complete this part of the formula: Σ(xi – x)2
16 + 9 + 1 + 1 + 9 + 16 = 52
So far, the sample standard deviation and population standard deviation formulas have been identical. At this point, they are different.
For the sample standard deviation, you get the sample variance by dividing the total squared differences by the sample size minus 1:
52 / (7-1) = 8.67
For the population standard deviation, you find the mean of squared differences by dividing the total squared differences by their count:
52 / 7 = 7.43
Why this difference in the formulas? Because in the sample standard deviation formula, you need to correct the bias in the estimation of a sample mean instead of the true population mean. And you do this by using n – 1 instead of n, which is called Bessels correction.
Finally, take the square root of the above numbers, and you will get your standard deviation (in the below equations, rounded to 2 decimal places):
| Sample standard deviation | Population standard deviation |
| â8.67 = 2.94 | â7.43 = 2.73 |
In Microsoft Excel, standard deviation is computed in the same way, but all of the above calculations are performed behind the scene. The key thing for you is to choose a proper standard deviation function, about which the following section will give you some clues.
Calculating standard deviation for text representations of numbers
When discussing different functions to calculate standard deviation in Excel, we sometimes mentioned “text representations of numbers” and you might be curious to know what that actually means.
In this context, “text representations of numbers” are simply numbers formatted as text. How can such numbers appear in your worksheets? Most often, they are exported from external sources. Or, returned by so-called Text functions that are designed to manipulate text strings, e.g. TEXT, MID, RIGHT, LEFT, etc. Some of those functions can work with numbers too, but their output is always text, even if it looks much like a number.
To better illustrate the point, please consider the following example. Supposing you have a column of product codes like “Jeans-105” where the digits after a hyphen denote the quantity. Your goal is to extract the quantity of each item, and then find the standard deviation of the extracted numbers.
Pulling the quantity to another column is not a problem:
The problem is that using an Excel standard deviation formula on the extracted numbers returns either #DIV/0! or 0 like shown in the screenshot below: 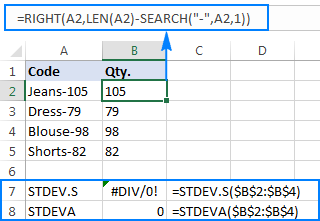
Why such weird results? As mentioned above, the output of the RIGHT function is always a text string. But neither STDEV.S nor STDEVA can handle numbers formatted as text in references (the former simply ignores them while the latter counts as zeros). To get the standard deviation of such “text-numbers”, you need to supply them directly to the list of arguments, which can be done by embedding all RIGHT functions into your STDEV.S or STDEVA formula:
=STDEV.S(RIGHT(A2,LEN(A2)-SEARCH("-",A2,1)), RIGHT(A3,LEN(A3)-SEARCH("-",A3,1)), RIGHT(A4,LEN(A4)-SEARCH("-",A4,1)), RIGHT(A5,LEN(A5)-SEARCH("-",A5,1)))
=STDEVA(RIGHT(A2,LEN(A2)-SEARCH("-",A2,1)), RIGHT(A3,LEN(A3)-SEARCH("-",A3,1)), RIGHT(A4,LEN(A4)-SEARCH("-",A4,1)), RIGHT(A5,LEN(A5)-SEARCH("-",A5,1))) 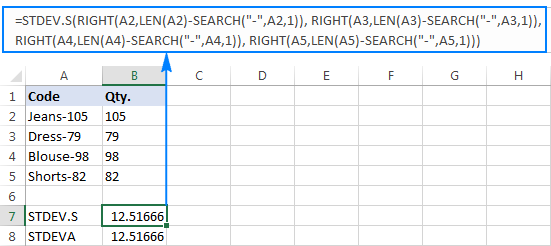
The formulas are a bit cumbersome, but that might be a working solution for a small sample. For a bigger one, not to mention the entire population, it is definitely not an option. In this case, a more elegant solution would be having the VALUE function convert “text-numbers” to numbers that any standard deviation formula can understand (please notice the right-aligned numbers in the screenshot below as opposed to the left-aligned text strings on the screenshot above): 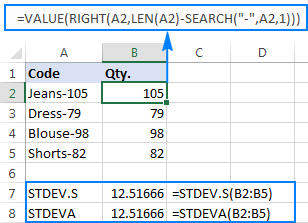
Standard Deviation in Excel (NEW VERSION IN DESCRIPTION)
How to calculate standard deviation in Excel?
Use STDEV.P for populations and STDEV.S for samples. The function will calculate the standard deviation for a selected range of cells. Enter the values you want to use. Pick a column in which you want to enter your data, then type each data value into individual cells in that column. Using Excel is a great way to organize and analyze your data.
How do I calculate standard deviation based on a numeric sample?
To calculate standard deviation based on a numeric sample, use the STDEV.S function in Excel 2010 and later; STDEV in Excel 2007 and earlier. To find standard deviation of a population, use the STDEV.P function in Excel 2010 and later; STDEVP in Excel 2007 and earlier.
Which Excel function estimates standard deviation based on a sample?
STDEV(number1,[number2],…) is the oldest Excel function to estimates standard deviation based on a sample, and it is available in all versions of Excel 2003 to 2019. In Excel 2007 and later, STDEV can accept up to 255 arguments that can be represented by numbers, arrays, named ranges or references to cells containing numbers.
How many functions are there to find standard deviation in Excel?
Overall, there are six different functions to find standard deviation in Excel. Which one to use depends primarily on the nature of the data you are working with – whether it is the entire population or a sample.